Logistic Classification 이론

Classification

Binary한 값을 예측하기 위한 모델: 이메일-스팸메일 구분, 페이스북 타임라인에서 특정 피드 보여주기-숨기기,  신용카드 도난 여부 확인, 주식 시장 예측

 

 

Binary한 값의 예측을 Linear Regression을 사용하여 하면 어떻게 될까?

 

예측값보다 큰 값으로 학습을 진행하면 그래프가 기울어지며 예측을 정확하게 하지 못한다.

따라서 Linear Regression 대신 0과 1 사이의 값으로 압축시켜주는 Sigmoid 함수를 도입한다.

 

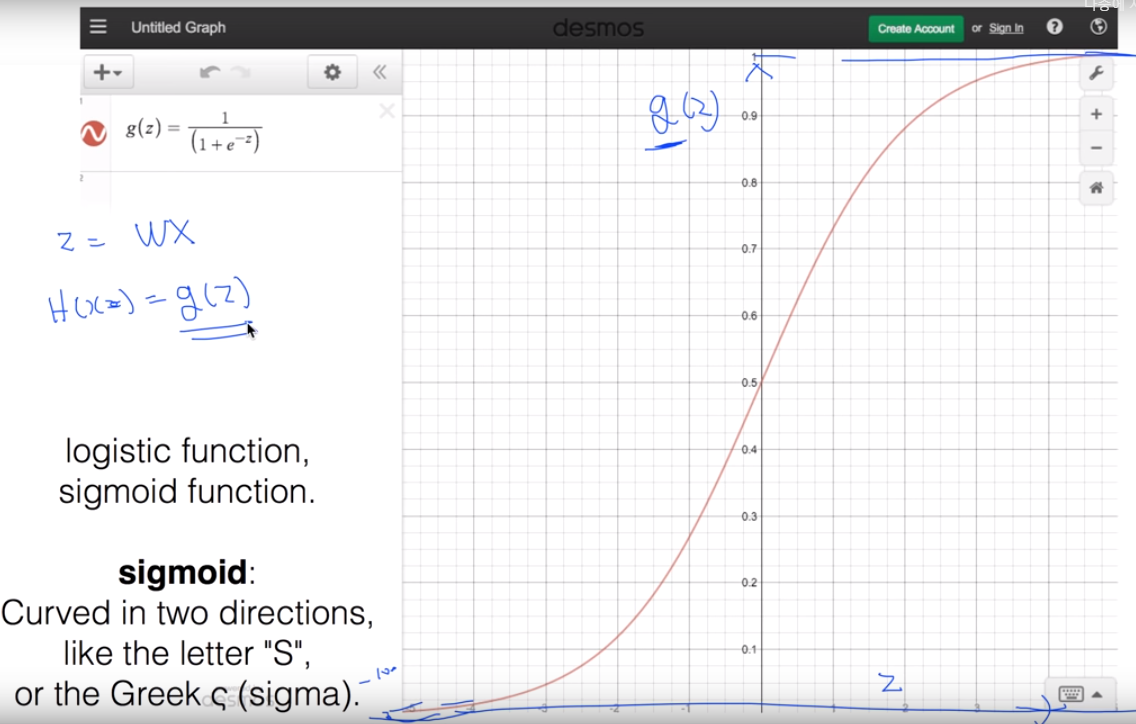
g(z) : 시그모이드 함수에 Hypothesis 함수를 합성하여 시그모이드 함수의 Hypothesis함수를 만들면 다음과 같이 나타난다.

 

 

 

Linear Regression의 가설과 비용함수를 다시 상기해보자.

 

가설 : H(x) = Wx+b

 

Cost Function : 

 

 

 

 

 

 

 

 

 

 

 

 

 

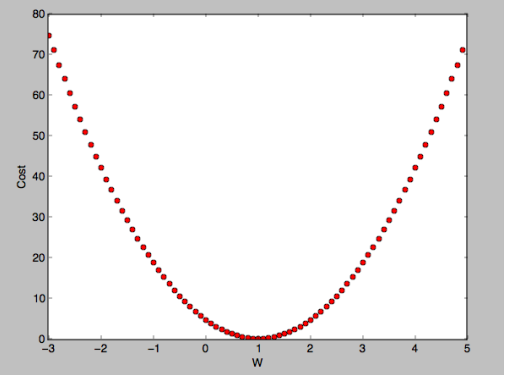
Linear Regression의 함수의 경우 아래로 볼록한 형태의 Convexfunction이므로 경사 하강법을 사용하여 구할 수 있었다.

 

 

 

이번에는 Logistic Regression의 가설과 비용함수를 정리해보자.

 

가설 : 

 

 

 

 

여기서 우리가 가설 함수를 Linear Regression의 Cost function에 집어넣으면 다음과 같은 그래프가 나온다.

위 그래프같은 경우 어떤 점에서 경사하강법을 사용하느냐에 따라 컴퓨터가 인식하는 cost minimum이 달라질 수 있다. 이런 함수는 non-convexfunction 함수이므로 우리는 Linear Regression의 costfunction이 convexfunction이 될 수 있도록 함수를 잘 정의해줘야 한다.

 

Cost Function : 

 

 

 

cost function을 다음과 같이 정의하겠다.

log함수를 사용하는 이유는 예측값과 실제값의 차이가 클 경우 예측 비용이 크도록 만들기 위해서 이다.

 

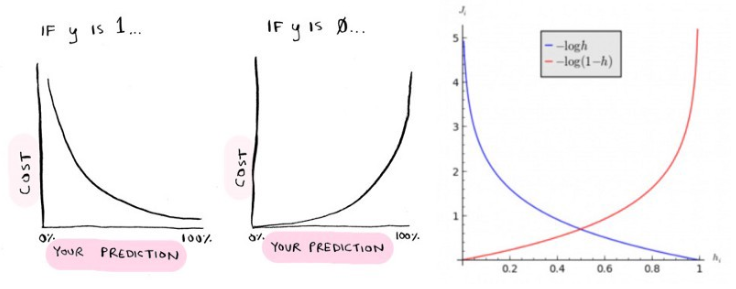
만약 실제 y=1이라면 H(x)가 1로 예측했다면 비용 C(H(x),y)=0이 나오지만 H(x)가 0으로 예측했다면 비용은 무한대가 된다.

 

마찬가지로 실제 y=0인데 H(x)가 0로 예측했다면 비용은 0이 나오지만 H(x)가 1로 예측했다면 비용은 무한대가 나온다.

 

 

 

 

cost function을 텐서플로우에 적용하기 쉽도록 if조건을 없애면 다음과 같이 표현이 되고,

이 함수의 그래프를 그리게 되면 convexfunction 형태의 그래프가 그려지게 된다.

 

이렇게 log를 사용해 그래프를 단순화 시키면 경사하강법을 사용하여 최소값을 찾을 수 있게 된다.

 

 

 

 

 

강의 출처 :  https://www.inflearn.com/course/%EA%B8%B0%EB%B3%B8%EC%A0%81%EC%9D%B8-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EB%94%A5%EB%9F%AC%EB%8B%9D-%EA%B0%95%EC%A2%8C/lecture/3388