Softmax Regression 이론

Multinomial Classification

 

  Linear Regression을 이용해 예측을 하였고, 이는 100, 200, -10 등의 어떤 하나의 실수 값을 예측 하는데는 유용한 모델이지만 Binary한 모델에는 적합하지 않다는 것을 보았다.

  그래서 예측값들을 Logistic Regression을 이용하여 0과 1사이의 수로 압축을 한 다음, 0과 1이라는 Binary한 값으로 예측을 하였다.

  이제는 Binary한 구분을 넘어 Multinomial한 구분을 하는 예측을 해보자.

 

입력 값 X를 넣고, W라는 unit을 가지고 계산을 해서 Z값이 나오고, 이를 Sigmoid 함수에 넣으면 0과 1사이의 값을 가지는 Y bar가 나온다. 

 

Logistic Regression을 학습시킨 다는 것은 2개의 구분선을 찾아낸다는 것이다. 직관적으로 표현하면 다음과 같다.

이 아이디어를 Multinomail 한 경우의 분류에도 적용할 수 있다.

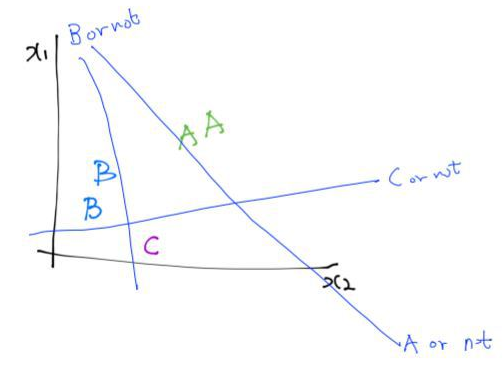
공부를 얼마나 했는지, 수업 참석은 잘 했는지에 따라 어떤 점수를 받을까에 대한 예제였다.

 

이 문제에서는 3개의 Binary Classification을 찾을 수 있다.

-A or not

-B or not

-C or not

 

 

 

 

 

이 3개의 Binary Classification을 수식으로 나타내면 다음과 같다.

 

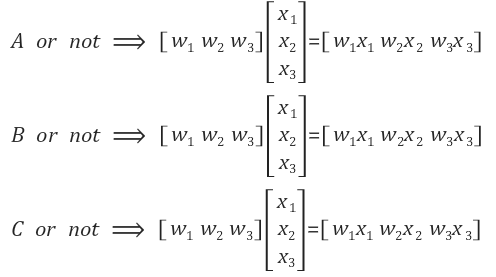
이 3개의 수식을 하나로 합쳐보자.

 

 

Signoid 함수에 이 행렬을 적용해보기!

 

위의 행렬을 통해 어떤 값을 연산했다고 하자. 그리고 다음과 같은 예측 값을 얻을 수 있었다고 해보자.

예측 값 중 2.0이 가장 크기 때문에 그 어떤 값은 A라고 예측할 수 있다. 하지만 우리는 sigmoid 함수를 사용하여 0~1 사이의 값으로 표현하는 것이다.

Softmax 함수를 사용하여 우리는 예측 값을 0과 1 사이의 값으로 변환하였다. 그리고 이 값들의 합은 1이라는 것도 알 수 있다. 이 값들의 합이 1이라는 것은 이것을 확률로서 볼 수 있다는 것이다. 

이와 같은 역할을 해주는 함수가 softmax 함수이고 이것을 구현하는 공식이 따로 있지만, 텐서플로우에서 함수를 호출해 구현할 수 있다.

 

 

이렇게 구한 예측값(y bar)을 '원 핫 인코딩'을 이용하여 가장 큰 값을 1로, 나머지 값을 0으로 바꿔준다. 이를 통해 어떤 값을 선택해야 하는지 명확히 구분된다. '원 핫 인코딩'에서 수행되는 로직이 간단하기 때문에 직접 코드로 구현해도 되지만, 텐서플로우에서는 argmax라는 함수를 제공한다.

 

 

여기까지 Hypothesis(가설)가 완성되었고, 다음 단계에서는 costfunction을 설계해보자.

 

 

Cross-Entropy

※ 일반적으로 regression에서는 SSE를 여전히 많이 쓰고, classification문제나 딥러닝에서는 cross entropy를 많이 사용한다.

 

S(y)는 예측값, L은 실제값을 의미한다.

Cost function이 적합한지 확인 해보자. A 또는 B 두가지의 값이 있고, 실제값이 B였다고 해보자.

그러면 A와 B 두가지로 예측하는 경우가 발생할 것이다.

Cost function은 맞았을때 작은 값, 틀렸을 때 큰 값을 반환하므로써 상, 벌을 주는 형식이라고 생각하면 된다.

다음과 같이 element-wise(요소별 연산)을 진행해 예시를 검증한다.

 

B인데 B라고 예측했을 경우

 

 

 

B인데 A라고 예측했을 경우

 

 

 

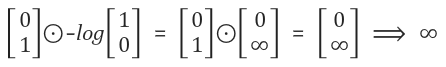
맞았을 때는 비용값이 적고, 틀렸을때는 비용값이 크다.

우리가 원하는 형태로 나왔고, Cost function이 제대로 작동했음을 알 수 있다.

 

 

※Logistic cost와 Cross entropy 두개의 식이 실제로는 같은 값을 의미한다.

왜 같은지 한 번 생각해보자.

 

 

 

 

 

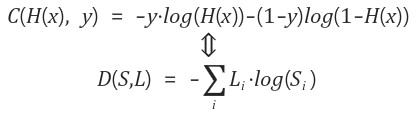
Cost function

여러개의 training set이 있을경우, 전체 거리를 더하고 그 수로 나누어 평균 거리를 구하면 된다. 그것이 전체의 cost function이다.

 

 

Gradient descent

경사하강법을 이용해 구하면 된다. 직관적으로 미분을 통해서 한다는 것을 알면 된다. 알파씩 내려가면서 찾아간다.

 

 

출처 :

https://www.inflearn.com/course/%EA%B8%B0%EB%B3%B8%EC%A0%81%EC%9D%B8-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EB%94%A5%EB%9F%AC%EB%8B%9D-%EA%B0%95%EC%A2%8C/lecture/3392

https://alsoj.tistory.com/128?category=708465